Часть 2. ЭПР-пары.
Может, это покажется занудством, но я считаю необходимым ещё раз уточнить, что же мы будем экспериментально проверять. Итак, у нас имеется система, включающая в себя протон и прибор, который может выдать только один из двух результатов измерения. Нам надо выяснить, имеется ли в этой системе скрытый параметр, предопределяющий результат измерения заранее. Встанем временно на сторону "детерминистов" и сделаем некоторые предположения о природе этого икс-параметра, или просто "X".
Во-первых, мы можем считать, что икс-параметр может иметь только два значения:
X = +1 (у тех протонов, которым суждено попасть в плюс-канал);
X = –1 (у тех протонов, которые попадут в минус-канал).
Или вообще можем считать, что X-параметр может быть либо положительным, либо отрицательным.
Во-вторых, мы знаем, что распределение X-параметра по ансамблю протонов зависит от угла α (напомню - это угол между направлением спина протона и ориентацией прибора).
Переведём эту фразу с "научного" на "русский". Ансамблем называют набор частиц, у которых одна или несколько характеристик идентичны. В нашем случае ансамбль - это набор протонов с одинаковым направлением спина. Например, такой ансамбль протонов мы получали в плюс-канале П1 в предыдущих опытах (рисунки 1.7, 1.9). А "распределение по ансамблю" - это среднее относительное количество протонов с положительным и отрицательным значением X-параметра в этом ансамбле. Например, мы знаем, что для всех протонов, у которых направление спина совпадает с ориентацией прибора, X-параметр положительный. А в ансамбле с α = 90° у половины протонов положительный Х-параметр, а у половины - отрицательный. По сути дела, получается, что формулы (ф. 1.3), (ф. 1.4) как раз определяют функцию распределения положительного и отрицательного Х-параметра по ансамблю протонов для всех возможных значений угла α.
Короче, в рамках классического подхода мы предполагаем, что результат прохождения протона через ПШГ определяется X-параметром, который, в свою очередь, зависит от угла α. При этом у разных протонов с одинаковым направлением спина форма зависимости X от α может быть различной.
В рамках квантового подхода мы полагаем, что результат прохождения протона через ПШГ – сугубо случайный процесс. Но вероятность получения того или иного исхода зависит от угла α. При этом все протоны с одинаковым направлением спина идентичны.
Какой из этих подходов правильный? Ответить на этот вопрос нам помогут ЭПР-пары частиц.
«ЭПР» означает «Эйнштейн, Подольский, Розен». Дело в том, что некогда эти трое физиков придумали парадокс, который должен был, по их представлению, показать неполноту квантовомеханического описания природы. В суть ЭПР-парадокса мы сейчас вникать не будем, скажем только, что в нём рассматривается поведение пары взаимосвязанных частиц. Предположим, что у нас есть некая частица «A», которая распадается на две частицы «B» и «C». Согласно закону сохранения, (векторная) сумма импульсов частиц «B» и «C» будет равна импульсу исходной частицы «A». В частности, если импульс частицы «А» в момент распада был равен нулю, то импульсы частиц «B» и «C» будут равны по абсолютной величине, но противоположны по направлению. То есть, импульсы продуктов распада – частиц «B» и «С», жестко взаимосвязаны. Вот эти взаимосвязанные частицы «B» и «C» и называют ЭПР-парой.
Момент импульса, или, в случае частиц – спин, тоже подчиняется закону сохранения. Значит, и спины частиц ЭПР-пары тоже жёстко взаимосвязаны. Если суммарный спин ЭПР-пары равен нулю, то спины каждой из частиц пары равны по величине и противоположны по направлению в пространстве. Мы будем иметь дело как раз с такими ЭПР-парами протонов. Такую пару можно получить, если выстрелить протоном в атом водорода. Впрочем, это процесс мы здесь изучать не будем, просто считаем, что у нас имеется источник ЭПР-пар протонов. Чтобы убедиться, что наш источник работает правильно и генерирует именно ЭПР-пары, проделаем следующий опыт (рисунок 2.1).
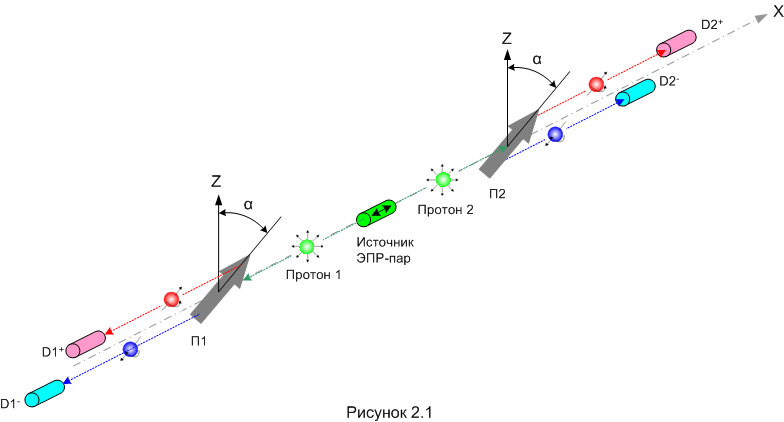
Источник ЭПР-пар, а также приборы Штерна-Герлаха П1 и П2 расположены вдоль одной оси, на рисунке это ось X. П1 и П2 могут поворачиваться вокруг оси X. В каждой попытке источник выпускает пару протонов. Один протон летит в П1, второй – в П2. В этом опыте мы ориентируем П1 и П2 параллельно, то есть поворачиваем их на одинаковый угол α относительно оси Z. Теперь сделаем серию «выстрелов» и убедимся, что детекторы всегда срабатывают «в противофазе». Если протон 1 уходит в плюс-канал П1 (срабатывает D1+), то протон 2 обязательно уходит в минус-канал П2 (срабатывает D2–). И наоборот, если протон 1 уходит в минус-канал П1, то протон 2 обязательно окажется в плюс-канале П2.
Повернём приборы на какой-нибудь другой угол и снова «постреляем» ЭПР-парами. Результат тот же: детекторы срабатывают в противофазе. И такой же результат будет для любого угла α. Мы убедились: если ориентации приборов П1 и П2 одинаковы, то результаты измерения спинов протонов жестко коррелируют между собой. Значит, мы действительно имеем дело с ЭПР-парами.
Раз уж я употребил такое учёное слово – «коррелируют», то я должен рассказать, что такое корреляция. Вы, конечно, и так знаете, что корреляция - это взаимосвязь между различными событиями, явлениями или процессами. Но корреляция может быть сильной и слабой, поэтому имеет смысл ввести количественную меру корреляции. Давайте сделаем это на нашем примере. Смотрите, в принципе, в опыте могло бы быть четыре исхода каждой попытки:
1) (+,+) – срабатывают детекторы D1+ и D2+;
2) (+,–) – срабатывают детекторы D1+ и D2-;
3) (–,+) – срабатывают детекторы D1– и D2+;
4) (–,–) – срабатывают детекторы D1– и D2–.
Если бы никакой корреляции между результатами измерения П1 и П2 не было, то все четыре исхода были бы равновероятны. Если бы была полная «положительная» корреляция (результаты измерений П1 и П2 всегда совпадают), то мы получали бы только исходы 1 и 4. Если бы была полная «отрицательная» корреляция, или, как ещё говорят – «антикорреляция» (результаты измерения всегда противоположны), то мы получали бы только исходы 2 и 3. В нашем опыте мы как раз наблюдали полную антикорреляцию. Но возможны ещё «промежуточные» случаи. Например, если бы в двух третях попыток мы бы получали исходы 1 или 4, а в оставшейся трети – исходы 2 или 3, то мы бы говорили о не полной, или не строгой корреляции. Из таких соображений в теории вероятности вводится такая величина – коэффициент корреляции. В нашем случае формула для вычисления коэффициента корреляции выглядит так:
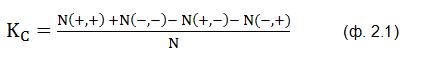 где:
где:
N(+,+) – количество попыток, когда оба у обоих приборов срабатывает плюс-канал;
N(–,–) – количество попыток, когда оба у обоих приборов срабатывает минус-канал;
N(+,–) – количество попыток, когда у П1 срабатывает плюс-канал, а у П2 – минус-канал;
N(–,+) – количество попыток, когда у П1 срабатывает минус-канал, а у П2 – плюс-канал;
N – общее количество попыток.
То же самое можно записать по-другому:
KC = P(+,+) + P(–,–) – P(+,–) – P(–,+) (ф. 2.2)
где символом «P» обозначены вероятности соответствующих исходов.
Видно, что для случая полной корреляции KC = 1. При полной антикорреляции KC = –1. Если корреляции нет совсем, тогда KC = 0. При неполной корреляции значение KC будет лежать где-то между нулём и ±1. Понятно, что чем слабее корреляция, тем ближе значение KC к нулю.
И ещё формулу для коэффициента корреляции можно записать так:
KC = P(совп) – P(разн) (ф. 2.3)
где
P(совп) = P(+,+) + P(–,–) вероятность совпадения результатов измерений;
P(разн) = P(+,–) + P(–,+) вероятность несовпадения результатов измерений.
В той форме неравенства Белла, которую мы дальше будем изучать, коэффициент корреляции в явном виде не используется. Но я хотел бы, чтобы вы чётко понимали, что такое корреляция и как она измеряется. К тому же, если вы захотите ещё чего-нибудь почитать по теме, эта информация пригодится.
Возвращаемся к нашим «баранам», то есть, ЭПР-парам протонов. Мы выяснили, что при одинаковой ориентации П1 и П2 коэффициент корреляции всегда равен минус-единице. А как будет обстоять дело при разной ориентации приборов? Выясним это с помощью следующего эксперимента (рис. 2.2).
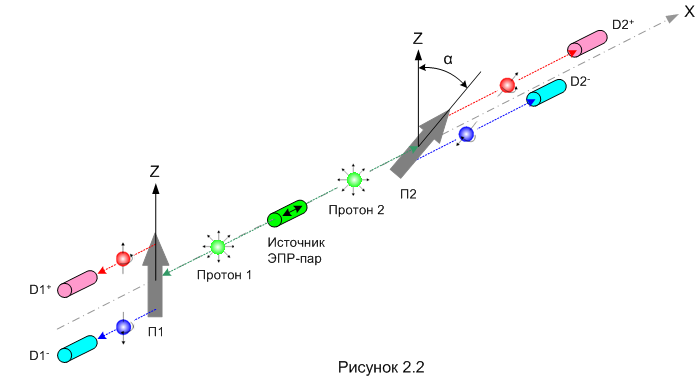
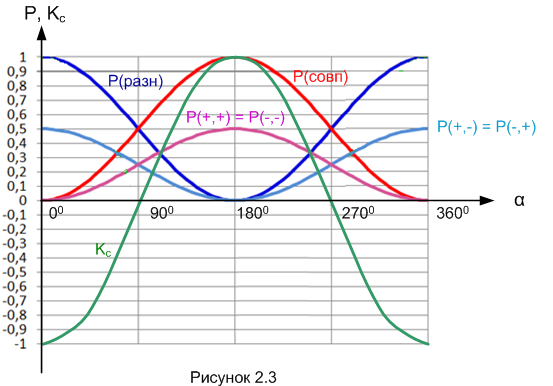
Схема та же, что и в опыте на рисунке 2.1. Но теперь мы сориентируем прибор П1 по оси Z и не будем его трогать. А прибор П2 будем поворачивать вокруг оси X на различные углы α Для каждого значения угла «отстреляем» длинную серию ЭПР-пар и посчитаем вероятности разных исходов, а также вероятности P(совп), P(разн) и заодно коэффициент коллеляции Kc. Потом построим график, как мы уже делали в одном из предыдущих опытов (рисунок 1.7 в первой части). Получится вот такая картина (рисунок 2.3).
А вот так будут выглядеть формулы для показанных на графике зависимостей:
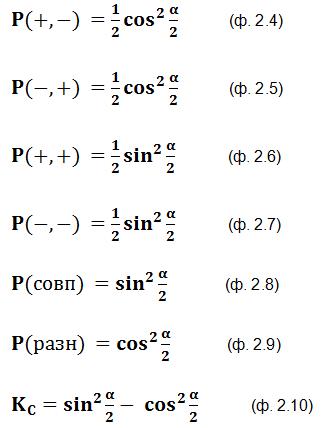
Вообще, все эти зависимости, полученные экспериментальным путём, мы могли бы вывести теоретически, используя формулы (ф. 1.3), (ф. 1.4), а также результаты опыта, показанного на рисунке 2.1. Но я не буду приводить здесь этот вывод, желающие себя проверить могут попробовать сделать это самостоятельно.
Отметим, что строгая антикорреляция между двумя протонами ЭПР-пар, точнее, между результатами измерений приборов П1 и П2, наблюдается при α = 0°, то есть, когда ориентации приборов совпадают. Строгая корреляция наблюдается при α = 180°, когда ориентации приборов противоположны. При α = 90° или α = 270°, когда ориентации приборов перпендикулярны, корреляции нет совсем. А при всех прочих значениях углов имеет место неполная корреляция. Вот эта самая неполная корреляция и послужит нам инструментом для разрешения спора между классическим и квантовым подходом.
Ну всё, теперь мы достаточно теоретически «подкованы», чтобы осмыслить неравенства Белла. Этим мы и займёмся в следующей части.
