Часть 3. Белловский экперимент
Мы выяснили на опыте, что результаты измерений спинов протонов ЭПР-пары коррелируют между собой. Но чем обусловлена эта корреляция?
Корреляция бывает, так сказать, двух "сортов". Во-первых, корреляция состояний двух различных объектов может объясняться тем, что оба объекта одинаково "запрограммированы". То есть, предполагаем мы, у каждого протона существует некий скрытый параметр, предопределяющий будущий результат измерения. Скрытый - потому что мы о природе этого параметра ничего не знаем. Но мы предполагаем, что параметры двух протонов ЭПР-пары взаимно согласованы, что и обеспечивает корреляцию результатов.
Во-вторых, корреляция может быть вызвана тем, что между объектами существует какая-то «оперативная» связь. Допустим, что изначально никакого параметра, предопределяющего результат измерения, нет. Для того протона, который первым достигает своего прибора, выбор осуществляется абсолютно случайно. Но второй протон тут же получает от первого некий сигнал и для него выбор уже предопределён.
Вроде как, это понятно, но на всякий случай объясню на следующем мысленном эксперименте "на людях". В опыте участвуют два испытуемых, допустим, Петя и Вася, и экспериментатор - ведущий. Пусть Петя и Вася сидят в разных комнатах. Ведущий ходит из одной комнаты в другую и задаёт испытуемым одинаковые вопросы. Испытуемые отвечают, и в ходе эксперимента выясняется, что ответы Васи и Пети всегда совпадают. То есть, между ответами наблюдается строгая корреляция. Как ведущий может объяснить такой результат? Тут возможны две версии.
Первая версия - и у Васи и Пети есть "справочник" (на бумаге или в голове), содержащий ответы на все мыслимые вопросы. Причём, совершенно не существенно, правильные это ответы или нет. Важно то, что оба справочника, и васин и петин, одинаковы. В данной ситуации эти справочники являются "скрытым параметром", предопределяющим ответы испытуемых. Скрытым - потому что ведущий о нём ничего не знает. Здесь причиной корреляции является то, что Петя и Вася действуют по одной заложенной в каждого из них «программе».
Вторая версия - Петя и Вася оперативно связываются друг с другом, допустим, телепатически. Скажем, ведущий спрашивает Васю: "Кто написал "Му-му"? У Васи никакого "справочника" нет, и он отвечает первое, что взбредёт в голову. Например: "Айвазовский". И немедленно после ответа Вася телепортирует Пете: "На вопрос "кто написал "Му-му", отвечай - Айвазовский". При таком раскладе корреляция между ответами Пети и Васи тоже обеспечена, но никакого скрытого параметра, заранее предопределяющего ответ, не существует.
В нашем опыте с ЭПР-парами ситуация аналогичная. Мы каждому протону из пары "задаём один и тот же вопрос", точнее, пропускаем протоны через одинаково ориентированные ПШГ. И тоже получаем полную корреляцию, только со знаком "минус". Протоны ЭПР-пары всегда "дают разные ответы": если один уходит в плюс-канал, то второй обязательно уйдёт в минус-канал. Здесь также возможны две версии объяснения этой корреляции.
С точки зрения классического «здравого смысла» напрашивается версия скрытого параметра - "программы". Как уже было отмечено выше, корреляцию параметров протонов должен обеспечивать классический закон сохранения момента импульса: если у системы, породившей два протона, был нулевой спин, то у протонов пары спины будут направлены противоположно. Значит, результаты измерений предопределяются в момент рождения ЭПР пары. Причём, если первому протону предопределено оказаться в плюс-канал П1, то второму предопределено оказаться в минус-канале П2. Конечно, при том условии, что П1 и П2 ориентированы одинаково. Всё выглядит пока вполне логично. Но давайте в рамках этой логичной классической версии спрогнозируем статистику измерений для разных ориентаций П1 и П2. И посмотрим, насколько эта статистика совпадает с результатами реальных экспериментов.
Эксперимент с разными ориентациями П1 и П2 мы уже проводили, смотрите рисунок 2.2 в предыдущей части. Для «белловского» эксперимента используем ту же схему, только чуточку «модернизируем» обозначения на ней (рисунок 3.1).
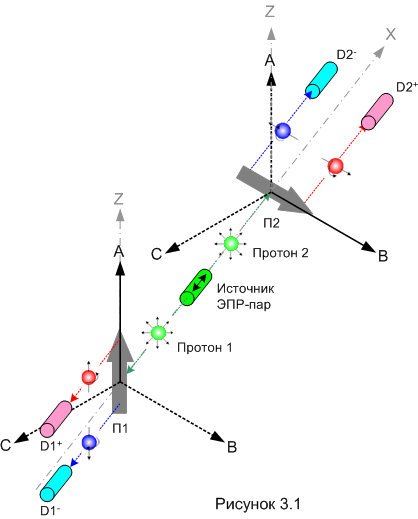
Приборы П1 и П2 по прежнему могут поворачиваться вокруг оси X. Но сейчас мы будем ориентировать их только в трёх направлениях, обозначенных на рисунке как A, B, C. На рисунке показана ситуация, когда прибор П1 ориентирован в направлении A, прибор П2 ориентирован в направлении B. Такую конфигурацию приборов мы обозначим так:
{A,B} – слева от запятой указана ориентация прибора П1, справа – ориентация прибора П2.
Аналогичным образом обозначим и другие возможные конфигурации: {A, C}, {A, A}, {B, A} и так далее.
Эксперимент будем проводить так. В каждой попытке случайным образом ориентируем приборы в одну из девяти возможных конфигураций, «выстреливаем» ЭПР-пару и фиксируем результат. Напомню, в эксперименте мы собираем статистику, поэтому попыток должно быть много, чем больше, тем лучше.
В каждой из шести конфигураций, в которых ориентации приборов не совпадают, возможны четыре исхода. Например, в конфигурации {A,B} показанной на рисунке 3.1, возможны следующие исходы:
[A+,B+] – в П1 и П2 сработали плюс-детекторы;
[A+,B–] – в П1 сработал плюс-детектор, в П2 сработал минус-детектор;
[A–,B+] – в П1 сработал минус-детектор, в П2 сработал плюс-детектор;
[A–,B–] – в П1 и П2 сработали минус-детекторы.
Аналогично будем обозначать исходы, полученные в прочих конфигурациях: [С+,B+], [В–,А+] и так далее. Не трудно посчитать, что всего для «разнонаправленных» конфигураций возможны 24 разных исхода.
В каждой из конфигурациях с одинаковой ориентацией приборов возможны только два исхода (кто не понял почему – освежите в голове результаты опыта на рисунке 2.1). Например, для ориентации приборов {A,А} возможны такие два исхода:
[A+,А–]
[A–,А+]
Исходы такого типа, коих для трёх «параллельных» конфигураций может быть всего шесть, мы в нашу статистику включать не будем. Но они послужат для контроля того, что наша экспериментальная установка работает правильно. Ведь, во-первых, если нам время от времени будут встречаться исходы типа [B+,B+] или [С–,С–], значит, наш источник ЭПР-пар или приборы «глючат», на одинаковых ориентациях приборов мы должны получать только противоположные результаты. Во-вторых, если после большого числа «выстрелов» обнаружится некоторый «перекос» в пользу одного из «параллельных» исходов, допустим, количество исходов [A+,А–] окажется значительно большим, чем количество исходов [B+,B–], то это будет означать, что спины протонов, выпускаемых ЭПР – источником, распределены по углу неравномерно. То есть, не совсем случайно. И «во-первых», и «во-вторых» делают недостоверными результаты всего эксперимента.
Теперь внимательно, переходим к ключевой задаче: выводу неравенства Белла. Попробуем предсказать результаты нашего эксперимента в рамках классического подхода. Мы предполагаем, что каждый протон ЭПР-пары несёт в себе X-параметр, однозначно предопределяющий результат прохождения ПШГ, ориентированного определённым образом. Иными словами, в протоне «записана» его реакция на любую ориентацию прибора. Скажем, в нашем эксперименте протон 1 может быть «запрограммирован», например, таким образом:
- в приборе с ориентацией {A} идти в плюс-канал (X = +1 для направления A);
- в приборе с ориентацией {B} идти в плюс-канал (X = +1 для направления B);
- в приборе с ориентацией {C} идти в минус-канал (X = -1 для направления С).
Эту «программу» будет удобно коротко записать так:
<A+,B+,C–>
Знак X-параметра для каждого направления показан соответствующим верхним индексом. Обращаю внимание: возможные конфигурации приборов мы обозначили фигурными скобками, результаты измерений – квадратными скобками, а возможные «программы» протонов – угловыми скобками.
Разумеется, в рамках таких классических «рассуждений» мы полагаем также, что в протоне «записано» значение X-параметра и для всех прочих направлений ориентации прибора. Но на результаты нашего эксперимента влияют значения X-параметра только для направлений A, B, C. С этой точки зрения все протоны мы можем разделить на восемь «сортов». Тут не буду «экономить бумагу» и перечислю их все:
<A+,B+,C+>
<A+,B+,C–>
<A+,B–,C+>
<A+,B–,C–>
<A–,B+,C+>
<A–,B+,C–>
<A–,B–,C+>
<A–,B–,C–>
Важно помнить ещё и то, что мы имеем дело с ЭПР-парами, в которых протон 1 и протон 2 для одинаково ориентированных приборов всегда дают противоположные результаты. Это должно означать, что X-параметры двух ЭПР-протонов для одного направления всегда противоположны по знаку. Например, если протон 1 «запрограммирован так: <A+,B+,C–>, то протон 2 обязательно «запрограммирован» противоположно: <A–,B–,C+>.
Теперь нам не составит большого труда вывести неравенства Белла.
Для начала поставим такой вопрос: какова вероятность получить тот или иной исход одного "выстрела"? Например, такой: [A+,B+]?
Очевидно, что такой исход может быть получен только если П1 ориентирован в направлении A, а П2 - в направлении B. То есть, в конфигурации приборов {A,B}.
Так же понятно, что этот исход могут дать только ЭПР-пары, в которых протон 1 несёт либо вот такой набор X-параметров:
<A+,B–,C+> ,
либо вот такой:
<A+,B–,C–>
Значит, формулу для вероятности исхода [A+,B+] мы можем записать так:
P[A+,B+] = P{A,B} * (P<A+,B–,C+> + P<A+,B–,C–>) (ф. 3.1)
Здесь P{A,B} - вероятность конфигурации {A,B}. У нас конфигурации переключаются случайным образом, и все 9 возможных конфигураций равновероятны. Следовательно:
P{A,B} = 1/9 (ф. 3.2)
P<A+,B–,C+>, P<A+,B–,C–> в формуле (ф. 3.1) - это вероятности генерации ЭПР-источником первого протона соответствующего сорта. Эти вероятности нам неизвестны, ну и не надо.
С учётом (ф. 3.2) формулу (ф. 3.1) мы можем переписать так:
P[A+,B+] = (1/9) * P<A+,B–,C+> + (1/9) * P<A+,B–,C–> (ф. 3.3)
Путём аналогичных рассуждений получим также следующие формулы:
P[B–,C–] = (1/9) * P<A+,B–,C+> + (1/9) * P<A–,B–,C+> (ф. 3.4)
P[A+,C+] = (1/9) * P<A+,B+,C–> + (1/9) * P<A+,B–,C–> (ф. 3.5)
Теперь сложим формулы (ф. 3.4) и (ф. 3.5):
P[B–,C–] + P[A+,C+] = (1/9) * P<A+,B–,C+> + (1/9) * P<A–,B–,C+> + (1/9) * P<A+,B+,C–> + (1/9) * P<A+,B–,C–> (ф. 3.6)
Сумма первого и четвёртого членов (выделены зелёным) в правой части выражения – это вероятность P[A+,B+], смотрите формулу (ф. 3.3). Тогда получается:
P[B–,C–] + P[A+,C+] = P[A+,B+] + (1/9)*P<A–,B–,C+> + (1/9)*P<A+,B+,C–> (ф. 3.7)
Значит, должно выполняться следующее неравенство:
P[A+,B+] ≤ P[B–,C–] + P[A+,C+] (ф. 3.8)
Это и есть искомое неравенство Белла.
Мы можем переписать его в таком виде:
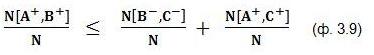 где:
где:
N[...] - количество попыток ("выстрелов"), в которых получен результат соответствующего вида;
N - общее количество попыток.
Теперь домножим все части на N и запишем неравенство Белла ещё проще:
N[A+,B+] ≤ N[B–,C–] + N[A+,C+] (ф. 3.10)
С точки зрения классического подхода это неравенство должно выполняться при любых направлениях A, B, C. Если на опыте выяснится, что это не так, значит, классический подход не состоятелен.
Теперь выведем аналогичное неравенство для квантового подхода. Он, напомню, заключается в следующем. Протон, подлетевший к прибору, не имеет "готовой программы", его спин не предопределён. Так что тот протон ЭПР-пары, который подлетел к своему прибору первым, "выбирает" плюс-канал или минус-канал случайно. При этом происходит "сеанс телепатии" между протонами ЭПР-пары: спин второго протона ориентируется строго противоположно тому направлению спина, которое измерено для первого протона. Например, если первый протон дал результат [A+], то второй немедленно переключится из неопределённого состояния в определённое состояние <A–>. Конечно, с "квантовой" точки зрения, это состояние определено только относительно прибора с ориентацией {A}. На прочих ориентациях прибора выбор опять будет случайным, предопределена только вероятность того или иного исхода. Короче, если один протон "выдал" результат [A+], то второй протон ведёт себя так, как будто бы он сам прошел через минус-канал прибора с ориентацией {A}. Или через плюс-канал прибора с противоположной ориентацией {–A}.
Рассчитаем теперь "квантовую" вероятность исхода [A+,B+]. Предположим, что первым сработал П1, а вторым – П2 (можно было бы предположить и обратное, на результат расчёта это не влияет). При таком раскладе вероятность исхода определяется произведением трёх вероятностей:
P[A+,B+] = P{A,B} * P[A+] * P(совп) (ф. 3.11)
Где
P{A,B} – вероятность того, что экспериментальная установка находится в конфигурации {A, B}. Выше мы выяснили, что эта вероятность равна 1/9.
P[A+] – вероятность того, что первый протон попадёт в плюс-канал П1. Здесь выбор абсолютно случаен, и эта вероятность всегда равна 1/2.
P(совп) – вероятность совпадения результатов П1 и П2 для данной взаимной ориентации приборов. Формула (ф. 2.8) для вычисления этой вероятности имеется в конце части 2. Перепишем её в следующем виде:
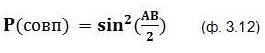 Здесь AB – угол между направлениями A и B.
Здесь AB – угол между направлениями A и B.
Теперь мы можем переписать формулу (ф 3.11) так:
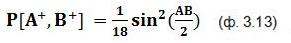
Рассуждая аналогичным образом, мы можем получить формулы для вероятностей следующих исходов:
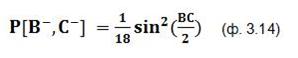
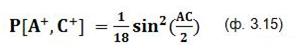
Теперь подставим полученные выражения (ф. 3.13), (ф. 3.14), (ф. 3.15) в неравенство Белла (ф. 3.8):
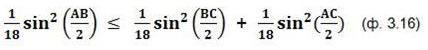
Общий множитель можем выбросить, тогда получится:
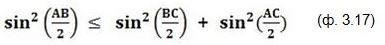
А теперь самый главный (в обсуждаемой теме) «квантовый» вывод: существуют такие взаимные ориентации направлений A, B, C, для которых это неравенство не выполняется.
Например, это неравенство не выполняется для следующей комбинации углов:
AB = 240°
BC = 60°
AC = 300°
Счастливые обладатели калькуляторов могут сами подставить эти углы в формулу (ф. 3.17) и убедиться :)
Значит, для такой взаимной ориентации направлений в реальных опытах не должно выполняться и неравенство (ф. 3.10). В виду практической важности выпишем это неравенство ещё раз:
N[A+,B+] ≤ N[B–,C–] + N[A+,C+] (ф. 3.10)
Ну что же, осталось только экспериментально проверить, какой подход, классический или квантовый, даёт правильные предсказания. Схема и методика эксперимента у нас уже описаны в начале этой части (рисунок 3.1). Выберем для опыта такой набор направлений A, B, C, для которого классический и квантовый подходы дают противоречащие друг другу предсказания. Отстреляем большое количество ЭПР-пар, аккуратно подсчитаем количество исходов [A+,B+], [B–,C–] и [A+,C+] и посмотрим, выполняется неравенство (ф. 3.10) или нет.
Так вот, такой реальный эксперимент показывает: неравенство Белла нарушается. Следовательно, «победа присуждается» квантовому подходу. А классический подход с его абсолютным детерминизмом и локальностью оказывается несостоятельным.
На этом можно было бы рассказ о неравенствах Белла закончить. Но я хочу высказать ещё несколько соображений на тему, поэтому окончание следует.
